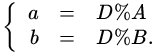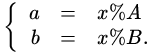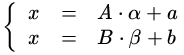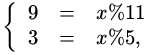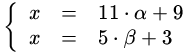pdf версия (для печати, обе стороны листа:
rsaa-pk.pdf,
нечетная сторона:
rsaa-1-pk.pdf,
четная сторона в обратном порядке:
rsaa-2-pk.pdf).
pdf версия для чтения с экрана телефона:
rsaa.pdf
Содержание
1 Вычисления в кольце вычетов 1.1 Сложение и умножение 1.2 Вычитание 1.3 Деление 1.3.1 Алгоритм нахождения обратного в кольце вычетов 1.4 Возведение в степень 1.4.1 Быстрый алгоритм возведения в степень 1.5 Извлечение корня 1.5.1 Алгоритм извлечения корня в в Zp, если p простое 1.6 Китайская теорема и извлечение корня 1.6.1 Как извлекать корни в Zp·q 1.6.2 Как обойтись без таблицы 1.7 RSA, Эль-Гаммаль и миллионер, но социалист2 Теория чисел 2.1 Деление с остатком 2.2 НОД и соотношение Безу 2.3 Алгоритм Евклида для НОД 2.4 Алгоритм Евклида для равенства Безу3 Всякая всячина 3.1 Проблема плохого начальника 3.2 Невозможное вычислениеIndex
Ответы на упражнения
Предметный указатель
1 Вычисления в кольце вычетов
Как известно, обычные числа
- это такая линеечка с делениями.
В обычных числах есть первичная операция "плюс один", или "на одно деление вправо", и
вторичные - сложение, умножение и возведение в степень.
Вторичные они потому, что
сложение
это многократное "плюс один",
умножение - многократное
сложение, и
возведение в степень - многократное
умножение.
Обычные числа - это очень просто, и поэтому для нужд криптографии
изобрели "ненормальные числа", в которых всё сложно.
Ненормальные
числа - это такой "циферблатик", т.е. линеечка, загнутая в кольцо.
Пример 1
На обыкновенных часах со стрелкой 12 делений, таким образом получается 12 чисел.
Ненормальные криптографы нумеруют их так: 0, 1, 2, ..., 11.
(А не 1, 2, ..., 12, как все нормальные люди).
Этот "циферблатик" называется кольцо вычетов с 12 числами
или
Z12.
Размеры "циферблатика" могут быть разными, т.е. существует много разных
систем ненормальных чисел.
1.1 Сложение и умножение
Арифметические операции с ненормальными числами в принципе такие же, но
первичная операция "плюс один" зацикливается, т.е. 11 "плюс один" будет 0.
Операции
сложения
, умножения
и
возведения в степень
определяются аналогично обычным числам.
Пример 2
10+5 = пять раз "плюс один" после десяти. Считаем пальчиком по циферблатику: 11, 0, 1, 2, 3.
Получается 10+5=3 в ненормальных числах Z12.
Пример 3
103 это 10·10·10. В свою очередь 10·10 это 10+10+10+10+10+10+10+10+10+10.
И в свою очередь 10+10 это (считаем пальчиком) 11, 0, 1, 2, 3, 4, 5, 6, 7, 8. Т.е. 10+10=8.
Продолжая считать пальчиком, когда-нибудь найдем 103.
Эти же действия можно сделать с помощью калькулятора.
Представим себе обыкновенные числа в виде верёвочки с узелками, а циферблат в виде бревна
с обхватом "12 узелков".
Теперь вычислять можно так: сначала отсчитываем узелки на верёвке, затем наматываем её на бревно
и смотрим, какой хвостик остался.
Пример 4
103
можно сосчитать на калькуляторе, получится 1000 (т.е веревочка, на которой тысяча узелков).
Наматываем: 1000 поделить на 12 (можно на калькуляторе) будет 83 с мелочью, т.е. 83 полных оборота
и хвостик. 83 полных оборота по 12 узелков будет 996, т.е. на хвостик остается 4 узелка.
Вот мы и сосчитали, 103=4 в ненормальных числах Z12.
Кстати, то, что мы только что проделали, называется деление с остатком
.
(см. раздел
2.1).
В равенстве 1000=12·83 + 4 число 1000 - делимое
,
12 - делитель
,
83 - частное
и 4 - остаток
.
Если пользоваться обозначениями из популярных языков программирования, то 1000%12=4
.
1.2 Вычитание
Напомним, что вычитание
- это операция, обратная к сложению, т.е.
a−
b=
c это то же самое, что и
a=
c+
b.
Немногие знают, что "черточка" в математике обозначает три разных вещи:
- Вычитание, т.е операция, обратная к сложению.
- Часть числа. Обычных чисел иногда не хватает, и люди придумали расширение - отрицательные числа.
К сожалению, бедные на фантазию математики обозначают их посредством пририсовывания черточки перед числом.
- Операцию взятия противоположного числа. Напомним, что два числа
называются противоположными, если
их сумма равна 0.
Как известно, 3 + (−3)=0, и это значит, что 3 противоположно −3 и −3 противоположно 3.
Присмотревшись к калькулятору с кнопочками, можно обнаружить там три "минуса": один справа в середине,
второй обычно внизу слева, и третий появляется на индикаторе при появлении там отрицательного числа.
В ненормальных числах всё немного не так.
Противоположные числа там уже есть изначально, так что пририсовывать черточку к числу не
нужно: 7+5=0 в
Z12 т.е. 7 - число противоположное к 5, а 5 - число противоположное к 7.
Присмотревшись к циферблатику, можно заметить, что противоположные
числа находятся
на противоположных (относительно вертикали) сторонах.
Напротив 2 находится 10, и действительно, 2+10=0 (в
Z12).
Операция вычитания как бы лишняя, потому что её можно заменить на прибавление противоположного,
для демонстрации чего и приведен
Пример 5
В нормальных числах −3 противоположно 3, и это значит, что вычитание x−3 можно заменить
на сложение x+ (−3). Аналогично в ненормальных числах: так как 7+5=0 (в Z12),
вычитание можно заменить на сложение: 3−7=3+5=8. Проверяем сложением: 8+7=15=12+3=3.
Упражнение 1
Решить уравнение x+3=2 в Z5.
1.3 Деление
Деление
- это операция, обратная к умножению.
Поскольку в
Z12 верно равенство 4·5 = 8, то 8/5=4.
Делить числа так, как мы раньше умножали и складывали, т.е. "поделить на веревочке и намотать",
(как в примере
4),
к сожалению, невозможно. 8/5=1.6 и на 4 совершенно не похоже.
Так же как и в случае с "черточкой", у математиков есть три вида "поделить":
- Обычное деление, на калькуляторе это кнопочка справа.
- Нахождение обратного. Обозначается x−1. На калькуляторе обозначается 1/x или x−1.
- "Запятая" на индикаторе калькулятора, что, как вы, наверное, помните, означает
несколько раз поделить на 10.
Напомним на всякий случай, что одно число называется обратным
к другому, если их произведение
равно 1, и вместо деления можно использовать умножение на обратное число.
Пример 6
В обычных числах 2·0.5=1, т.е. 2 обратно к 0.5 и 0.5 обратно к 2.
И теперь можно делить умножением: a/2=a·0.5 и a/0.5=a·2.
Примерно так мы и будем делить в кольце вычетов.
Пример 7
Произведение 3·4 = 12 = 11+1 т.е. 3·4 = 1 в Z11.
Следовательно, мы внезапно научились делить на 3 и на 4 в Z11:
2/3=2·4 = 8, 2/4=2·3 = 6, 5/3=5·4 = 20 = 9 и т.д.
С обратными числами в кольцах вычетов всё не просто.
Пример 8
Проведем
исследование в Z6, для этого перемножим всевозможные числа (кроме 1 и 0):
2·2 = 4 ,
2·3 = 6 = 0 ,
2·4 = 8 = 6+2 = 2 ,
2·5 = 10 = 6+4 = 4 ,
3·3 = 9 = 6+3 = 3 ,
3·4 = 12 = 6·2+0 = 0,
3·5 = 15 = 6·2+3 = 3 ,
4·4 = 16 = 6·2+4 = 4 ,
4·5 = 20 = 6·3+2 = 2 ,
5·5 = 25 = 6·4 + 1 = 1.
Как видите, не у всех чисел есть обратное (5 обратно 5, но у других чисел обратного нет),
да и у тех, у которых есть, совершенно не
ясно, как это самое обратное находить.
Понятно, что находить обратное тупым перебором можно в маленьких кольцах вычетов, но нельзя в больших.
В популярном в криптографических кругах
Zстозначное число, перебор
всех вариантов
(как показано в разделе
3.2)
вообще никогда не не закончится.
Сейчас вы узнаете достаточно быстрый
1.3.1 Алгоритм нахождения обратного в кольце вычетов
Он основан
на соотношении Безу, про которое можно (и нужно) почитать в разделе
2.2.
Предположим, некто заставляет нас найти
A−1 в кольце вычетов
ZN.
Заставим кого-нибудь (кто уже прочитал раздел
2.2) найти для нас числа
u и
v в
соотношении Безу
Нам нужно то соотношение, в котором число
u положительное и
v
отрицательное (см. утверждение
6).
Если НОД получился не 1, то это хорошо, обратного не существует.
Так этому Некту и говорим, и идем отдыхать.
Если НОД равен 1, то это плохо, придется считать дальше.
Преобразуем это соотношение Безу
в равенство
Отчетливо видно, что слева умножение двух чисел, а справа формула деления с остатком.
Вот мы и нашли обратное, это будет
u.
Пример 9
Найдем 3−1 в Z11. Нам принесут 3·4 + 11·(−1)=1.
Делаем вывод: 3−1=4. Делаем проверку: 3·4 = 12 = 11 +1.
Ах да, если тот самый кто-нибудь принес нам соотношение Безу со слишком большими
числами, (например 3·15 + 11·(−4)=1), то придется это обратное "намотать на бревно"
(15=11+4=4 в
Z11), чтобы оно помещалось в кольцо вычетов.
Упражнение 2
Решить уравнение 33·x + 25 = 0 в кольце вычетов Z41.
1.4 Возведение в степень
Возведение
в степень - это
многократное умножение, как все знают.
Также все знают, что возводить в большую степень нет смысла, получается
очень большое число, которое ни в какой компьютер не поместится.
Но в кольце вычетов слишком больших чисел не бывает.
Ибо даже стозначное число в стозначной
степени в стозначном кольце вычетов - всего лишь стозначное число, и оно почти в любом
компьютере помещается.
Проблема в том, что проделать стозначное число умножений невозможно.
(Про это написано в разделе
3.2).
Оказывается, есть более
1.4.1 Быстрый алгоритм возведения в степень
Проиллюстрируем
его идею на примере:
x6 =
x·
x·
x·
x·
x·
x, т.е. пять умножений.
Но если схитрить:
x6=(
x3)
2=(((
x2)·
x)
2), то понадобится только три умножения.
Может показаться, что три не намного лучше чем пять, но при больших степенях
разница становится впечатляющей,
x1024 можно сосчитать за 1023 умножения, а можно
вспомнить, что 1024=2
10, и сосчитать за десять возведений в квадрат.
Погуглив в Википедии
1, можно
узнать, что количество умножений
при этом быстром возведении в степень не более чем в два раза больше, чем
длина двоичной записи степени.
Стозначное десятичное число - это не более чем 400 значное двоичное и,
следовательно, для возведения в стозначную степень нужно сделать не более 800 умножений.
Почти любой компьютер с этим легко справится.
1.5 Извлечение корня
В
обычных числах корень извлекают
методом
половинного деления
2.
Поскольку в кольце вычетов слова "одно число правее другого" не имеют
смысла, то и метод половинного деления не работает.
Есть ли другие методы извлечения корня (кроме тупого перебора, конечно)?
Это сложный вопрос, ответ на который пока не найден.
Но в некоторых специальных случаях такой алгоритм существует, и про него вы сейчас прочитаете.
Напомним, что число называется
простым, если оно ни на что не делится (кроме 1 и самого себя).
Так вот, если в кольце вычетов количество чисел простое число (
Z2,
Z3,
Z5,
Z7, ...),
то у такого кольца вычетов появляются некоторые приятные свойства.
Например, у всех чисел (кроме 0) есть обратное
(см. раздел
1.3.1), если произведение двух
чисел равно 0, то одно из них 0 (но в
Z6, как показано в примере
8, это не так),
и еще кое что.
Но нас будет интересовать
Утверждение 1 [Малая теорема Ферма]
Если
p простое число, то в Zp, для всех чисел x из Zp (кроме 0),
выполнено равенство
Пример 10
В Z3 выполняется: 12=1, 22=4=3+1=1.
В Z5 выполняется: 14=1, 24=16=15+1=1, 34=(32)2=42=1, 44=(42)2=12=1.
Но в Z4 не выполняется: 23=8=0 , 33=9·3 = 1·3 = 3.
Благодаря этому самому Ферма, у нас есть
1.5.1 Алгоритм извлечения корня в в Zp, если p простое
Он
работает в два шага:
предположим, некто дал нам задание найти
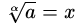
в
Zp.
- Найдем обратное к степени (т.е. к α) в Zp−1 (внимание, там написано на единицу меньше).
Если обратного нет, то это значит, что этот алгоритм применять нельзя. Так
этому Некту и говорим и идем отдыхать.
Но если обратное всё-таки есть, придется переходить к шагу два.
-
Итак, мы нашли обратное т.е. β·α = 1 в Zp−1.
Теперь, вместо извлечения корня степени α, мы будем возводить a в степень β.
(Внимание, вычисления проводятся опять в исходном кольце вычетов Zp).
Следующее предложение весьма важно, и поэтому мы поместим его в рамочку:
|
Оказывается, aβ = x в Zp. |
Напоминаем, что у нас есть (см. раздел 1.4) быстрый алгоритм возведения
в степень, его и следует применять.
Пример 11
Найдем
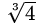 в Z11.
в Z11.
- Найдем 3−1 в Z10 так, как это сделано в разделе 1.3.
Если вы всё сделаете правильно, то у вас получится 3−1=7. Проверим на всякий случай: 3·7 = 21 = 10·2 + 1.
- Возводим 4 в седьмую степень в Z11:
47=(42·4 )2·4 = (16·4 )2·4 = (5·4 )2·4 = 202·4 = 92·4 = 81·4 = 4·4 = 16 = 5
Итак, ответ
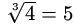 в Z11.
Сделаем проверку: 53 = 5·5·5 = 25 ·5 = 3 ·5 = 15 = 4.
в Z11.
Сделаем проверку: 53 = 5·5·5 = 25 ·5 = 3 ·5 = 15 = 4.
Разоблачение фокуса:
нам нужно, чтобы
xα =
a в
Zp.
У нас β·α = 1 в
Zp−1, на обычном языке это означает,
что остаток от деления равен 1, т.е.
выполнение равенства β·α = (
p−1)·
t + 1.
Итак:
xα = (
aβ)
α =
aβ·α=
a(p−1)·t + 1 = (
a(p−1))
t ·
a1.
И, по малой теореме Ферма (утв.
1),
a(p−1)=1 в
Zp, и всё доказано.
Упражнение 3
Убедитесь, что в Z12 этот алгоритм не работает (и не должен, 12 не простое число).
Кстати, из теоремы
1 следует
Утверждение 2 [Про возведение в степень и p−1]
Если
два числа (a и b) отличаются друг от друга на p−1 (т.е. a=b+α·(p−1)),
то в Zp (p - простое число) возведение в степень a и возведение в степень b это одно и то же.
Действительно, так как
xp−1=1, выполняется равенство:
xa =
xb+α·(p−1) =
xb ·(
xp−1)
α =
xb ·1
α =
xb .
Упражнение 4
Найдите 222222222222222222222222 в Z11.
Можно ли это вычислить без калькулятора и перерывов на сон и еду?
1.6 Китайская теорема об остатках и извлечение корня
Кроме нормальных чисел (в виде линеечки с делениями) и ненормальных колец
вычетов (в виде циферблатика),
существует еще более хитрое вычислительное устройство
в виде "велосипедика"
3.
Представьте себе две звездочки, соединенные цепью примерно как у велосипеда.
Их вращение синхронизировано так, что поворот на один зубчик одной звездочки
приводит к повороту на один зубчик другой звездочки.
На зубцах звездочек написаны числа совсем как у кольца вычетов.
Звездочки на заводе установлены в положение (0,0), т.е. левая звездочка в
положении 0 и правая тоже в положении 0.
Операция "плюс один" в этом "велосипедике" - это поворот обеих звездочек на один зубчик.
Если делать "плюс один" несколько раз, то положение звездочек будет меняться: (1,1), (2,2), ...
Дальше всё зависит от размеров звездочек, если они одинакового размера, то ничего интересного
происходить не будет, получится обычное кольцо вычетов в двух экземплярах.
Но если их размеры разные, то получится примерно так:
Пример 12
Пусть
, для примера, на левой звездочке три зубца, а на правой четыре.
Тогда положения звездочек будут меняться так:
0−(0,0),
1−(1,1),
2−(2,2),
3−(0,3),
4−(1,0),
5−(2,1),
6−(0,2),
7−(1,3),
8−(2,0),
9−(0,1),
10−(1,2),
11−(2,3).
И потом опять
(0,0),
(1,1), ...
Присмотревшись, можно заметить, что звездочки проходят через все возможные
комбинации в странном порядке и потом возвращаются в исходное положение.
Оказывается верно
Утверждение 3 [Китайская теорема об остатках в облегченной формулировке]
Если на левой звездочке A зубчиков, на правой B и эти числа
взаимно просты (т.е. НОД(A,B)=1), то операция "плюс один"
переведет звездочки через всевозможные комбинации, и комбинаций этих будет A·B штук.
Более того, верно
Утверждение 4 [Продолжение Китайской теоремы]
Если пронумеровать эти комбинации пар чисел в том порядке, в котором
они появляются, то этот велосипедик будет работать так же, как и обыкновенное
кольцо вычетов4 ZA·B.
Про "будет работать так же" следует пояснить:
вот представьте, что у нас на стеклянной стене карточки, у которых с одной стороны
написаны пары чисел от "велосипедика", а с другой их номер, т.е. числа из большого
кольца вычетов (посмотрите на пример
12). Если теперь производить всякие там арифметические действия
с числами из большого кольца вычетов, то люди с другой стороны стеклянной стены
будут думать, что эти действия производятся с парами чисел "покоординатно".
Пример 13
Вычислим 2+3 в Z12 и вычислим покоординатно (2,2)+(0,3) в велосипедике (см. пример 12).
На одной стороне стеклянной стены будет 2+3=5, на другой (2,2)+(0,3) = (2+0,2+3) = (2,1).
Но у карточки с парой чисел (2,1) на другой стороне как раз и написано 5.
Пример 14
Вычислим 32 в Z12 и вычислим покоординатно (0,3)·(0,3) в велосипедике (и опять см. пример 12).
На одной стороне доски будет 3·3 = 9, на другой (0,3)·(0,3) = (0·0,3·3) = (0,1).
Но у карточки с парой чисел (0,1) на другой стороне как раз и написано 9.
Благодаря этому вот наблюдению, алгоритм
извлечения корня из раздела
1.5
можно применять в кольцах вычетов
Zp·q, где
p и
q простые числа.
И сейчас вы узнаете
1.6.1 Как извлекать корни в Zp·q
- Мысленно строим таблицу соответствий между Zp·q и "велосипедиком" со
звездочками Zp и Zq.
-
Ищем в этой таблице пару, соответствующую нашему числу.
-
Вместо извлечения корня из числа в большом кольце вычетов, будем
два раза извлекать корень из двух чисел в двух маленьких кольцах вычетов.
Это можно и нужно делать по алгоритму из раздела 1.5.1 так как p и q простые числа.
-
Потом опять посмотрим в таблицу и найдем число, соответствующее паре этих самых корней. Это и будет ответ.
Пример 15
Числа
11 и 5 простые.
Возьмите большой-пребольшой лист бумаги и запишите на него таблицу с 11·5 = 55 числами.
У вас должно получиться как-то так:
0−(0,0),
1−(1,1),
2−(2,2), ...
5−(5,0),
6−(6,1), ...
11−(0,1),
12−(1,2), ...
54−(10,4).
Число 3 взаимно просто с 10=11−1 и 4=5−1, так что
извлечь корень 3 степени у нас получится.
Возьмем первое попавшееся число, например, 53.
Посмотрев в большую таблицу, увидим, что числу 53 соответствует пара (9,3).
Теперь будем два раза извлекать корень, так, как это
сделано в примере 11.
Если вы все сделаете правильно, то у вас получится:
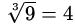 в Z11 и
в Z11 и
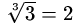 в Z5.
(В этом месте желательно сделать проверку:
43=16·4 = 5·4 = 20 = 9 в Z11 и
23=8=3 в Z5).
И опять посмотрев в таблицу, увидим, что паре (4,2) соответствует число 37.
На всякий случай сделаем проверку (см. упр. 6): сосчитав на калькуляторе
(37·37 ·37 − 53 ) / 55,
обнаружим, что получилось целое число. Значит, все правильно.
в Z5.
(В этом месте желательно сделать проверку:
43=16·4 = 5·4 = 20 = 9 в Z11 и
23=8=3 в Z5).
И опять посмотрев в таблицу, увидим, что паре (4,2) соответствует число 37.
На всякий случай сделаем проверку (см. упр. 6): сосчитав на калькуляторе
(37·37 ·37 − 53 ) / 55,
обнаружим, что получилось целое число. Значит, все правильно.
Вероятно, вам не понравилось рисование гигантских таблиц, и сейчас вы узнаете,
1.6.2 Как обойтись без таблицы
Итак, у нас есть "велосипедик" из
ZA и
ZB.
Заметим, что выписывание пар чисел по порядку есть не что иное, как
наматывание двух веревочек на два бревна.
Так что пара (
a,
b), соответствующая большому числу
D, есть просто остатки от деления.
И действительно, 53%11 = 9 и 53%5 = 3.
В обратную сторону несколько сложнее.
Предположим, у нас есть пара чисел (
a,
b) в "велосипедике" из
ZA и
ZB, и нам нужно найти
число
x из большого кольца вычетов, которое соответствует
этой паре, т.е. нужно решить систему уравнений
Вспомним, что такое остаток
от деления
и приравняем правые части уравнений
Ясно, что если мы найдем α или β, то найдем и
x.
Перенесем неизвестные влево и известные вправо
Ой, это же почти что соотношение Безу
! (см. раздел
2.2).
Ну теперь уравнение легко решить.
Пример 16
Пусть
у нашего велосипедика звездочки с 11 и 5 зубчиками, и
нам надо найти соответствие паре (9,3).
Система уравнений будет такая
потом такая
и уравнение получится такое
|
11·α+ 5·(− β) = 3 − 9 = −6. |
| (2) |
Найдем соотношение Безу (см. раздел 2.4)
Если его умножить на −6
|
11·(1·(−6) ) + 5·(−2·(−6)) = 1·(−6) , |
|
то получится как раз равенство (2)
Упс. Не получается. α и β получились отрицательными. Плохо. Что же делать?
Придумал! Нужно попробовать другое соотношение Безу, с другими знаками.
(Как его найти, написано в утверждении 6).
Умножаем на −6
и сравниваем с формулой 2.
Вот мы и нашли, α = 24, β = 54.
Подставив α = 24 в верхнее уравнение (1),
найдем x = 11·24 + 9 = 273.
Подставив β = 54 в нижнее уравнение (1),
найдем x = 5 ·54 + 3 = 273. Совпадает, это хорошо.
Более того, 273 = 55 ·4 + 53 = 53 в Z55,
совсем как в примере 15.
Упражнение 5
Убедитесь, не заглядывая в таблицу, что в примере 15
паре (4,2) действительно соответствует число 37.
1.7 RSA, Эль-Гаммаль и миллионер, но социалист
Погуглив эту абракадабру, вы погрузитесь в загадочный мир современной криптографии,
и с удивлением обнаружите, что вам почти всё понятно!
Секретный ключ в RSA - это
два простых числа (достаточно больших, стозначных например),
публичный ключ - это их произведение, шифрование - это
возведение сообщения в степень (обычно в третью) в кольце вычетов,
а дешифрование - это извлечение корня, про которое вы только что прочитали в разделе
1.6.
И даже загадочные "Схема Эль-Гамаля"
и
задача миллионера-социалиста
5
покажутся не такими уж и непонятными после чтения
раздела
1.3.1 про обратные числа и
1.4.1 про быстрое возведение в степень.
2 Теория чисел
Из этой главы вы узнаете кое-что про целые числа.
Напомним, что целые
числа это ...,−3,−2,−1,0,1,2,3,4,..., и их можно
представлять себе как очень очень длинную линеечку с делениями.
На этих числах есть первичная операция "плюс один" или "на одно деление вправо", и
вторичные - сложение, умножение и возведение в степень. Вторичные они потому, что
сложение это многократное "плюс один", умножение - многократное сложение, и
возведение в степень - многократное умножение.
Кроме этого, у вышеперечисленных операций есть обратные: вычитание, деление и извлечение корня,
впрочем, всё это вы, вероятно, проходили в школе.
2.1 Деление с остатком
Деление с остатком
проходят в школе.
Напомним, что равенство вида
называется делением числа
A на число
B с остатком.
Точнее,
A - делимое
,
B - делитель
,
C - частное
и
R - остаток
.
Остаток (т.е.
R) должен быть меньше частного (т.е.
B), иначе нещитово.
Это равенство можно представлять себе как наматывание веревочки длиной
A на бревно с обхватом
B.
Получится
C полных оборотов и "хвостик"
R.
Пример 17
Если веревочку длиной 7 наматывать на бревно с обхватом 3, то получится
два полных оборота и "хвостик" длины 1.
Это можно записать формулой 7=3·2+1, или сказать, что остаток от
деления 7 на 3 равен 1.
В дальнейшем, нам особенно часто придется находить остаток от
деления, и поэтому мы будем пользоваться обозначением из популярного языка
программирования:
A%
B =
R.
При нахождении остатка от деления на обыкновенном калькуляторе
приходится записывать целую часть частного на бумажку и потом
вводить обратно в калькулятор. И это неудобно.
Но зато проверку можно делать не отрывая рук от калькулятора:
Упражнение 6
Докажите
, что для проверки равенства A%B = R достаточно вычислить ( A−R )/ B.
Если получается целое число, то всё в порядке, если не целое, то не в порядке.
Упражнение 7
Определите, какое из равенств верно, ничего не записывая на бумажку:
1234%567 = 100 или 1234%567 = 101?
2.2 Наибольший общий делитель и соотношение Безу
Будем говорить, что одно число
делится
на другое, если оно делится нацело, т.е. без остатка.
Например, 12 делится на 4 (12/4=3) и не делится на 5 (12/5=2.4).
То число, на которое делится другое число, называется
делителем.
Например, 4 делитель 12, но 5 не делитель 12.
Наибольший общий делитель (НОД) - это
наибольшее число, являющееся общим делителем
(Капитан Очевидность одобряет это определение).
Пример 18
Число 12 делится на 1, 2, 3, 4, 6 и 12.
Число 8 делится на 1, 2, 4 и 8.
Таким образом, НОД(12,8)=4.
Если НОД двух чисел равен 1, то говорят, что они
взаимно просты.
Поиск НОД тупым перебором возможен у маленьких чисел и невозможен у больших.
(Про это написано в разделе
3.2).
Более того, поскольку при нахождении НОД нужно искать "самое большое из возможных",
то возникает "проблема плохого начальника",
(про него написано в разделе
3.1),
которую, в данном случае, можно решить с помощью соотношения Безу, и сейчас вы узнаете, как это сделать.
Утверждение 5
Оказывается, если НОД(A,B)=N, то можно найти пару целых чисел u, v (одно из них отрицательное) таких, что
Это равенство и называется соотношение Безу.
Пример 19
Вот типичное соотношение Безу:
12·1 + 8·(−1)=4.
Польза от этого самого соотношения Безу следующая:
предположим, плохой начальник
заставляет вас найти
наибольший общий делитель чисел 1234567 и 89101112.
Вы приносите ему 1.
"Ну хорошо", говорит начальник, "эти числа действительно делятся на 1,
но какие ваши доказательства, что они больше ни на что не делятся"?
А если вы принесете ему
|
1234567·76257319 + 89101112·(−1056606 )=1, |
|
то сделав два умножения и одно вычитание, начальник убеждается, что равенство верно, и
автоматически получает доказательство
того, что
|
|
НОД
| (1234567,89101112)=1. |
|
Ибо если бы эти числа делились на другое число, на это другое число делилось бы и
число 1234567·76257319, число 89101112·(−1056606 ) и
число
|
1234567·76257319 + 89101112·(−1056606 ), |
|
а оно равно 1 и на другие числа не делится.
На всякий случай запомните: соотношение Безу находится неоднозначно.
Т.е. если начальник даст одинаковые числа разным людям, то они могут найти
разные, но правильные соотношения Безу.
Пример 20
Вот два разных но правильных соотношения Безу:
3·(−1) + 4 ·(1) = 1 и 3·(3) + 4 ·(−2) = 1.
Перейти от одного соотношения Безу к другому можно с помощью следующего приёма:
Утверждение 6
Если
A·(u) + B·(v) = N то A·(u−B) + B·(v+A) = N
и A·(u+B) + B·(v−A) = N.
Для доказательства достаточно раскрыть скобки.
Пример 21
Берем вот такое 3·(−1) + 4 ·(1) = 1 соотношение Безу, прибавляем и
вычитаем: 3·(−1+4) + 4 ·(1−3) = 1,
и получаем 3·(3) + 4 ·(−2) = 1.
Кстати, таким методом можно переставить минус в соотношении Безу,
иногда
(в примере
16)
это важно.
Итак, у вас остались два вопроса:
- Как искать НОД быстрее чем методом перебора?
- Как находить числа в равенстве Безу?
2.3 Алгоритм Евклида для нахождения наибольшего общего делителя
Заметим, что если некие числа делятся на
x, то их суммы, разности и произведения тоже будут делиться на
x.
Например, 12, 9 и 15 делятся на 3.
Легко проверить на калькуляторе, что 12 + 9, 12 − 9, 15·12 +9 тоже делятся на 3,
И даже 12·7 и 15·5 − 9 делятся на 3, хотя 7 и 5 на 3 не делятся.
Основываясь на этом наблюдении, проделаем следующее странное действие:
поделим одно число на другое с остатком:
A=
B·
C +
R (
A - делимое,
C - делитель
R - остаток).
Следовательно, делители
R и
B будут делителями
A.
Это же равенство можно записать через разность:
R=
A−
B·
C.
И, следовательно, делители
A и
B будут делителями
R.
Таким образом, мы нечаянно доказали
Утверждение 7 [Теорема Евклида о НОД]
Если A%B = R, то НОД(A,B)=НОД(B,R).
Которое позволяет свести сложную задачу поиска НОД для больших чисел
A и
B к чуть менее сложной задаче
поиска НОД для чуть меньших чисел
B и
R (напомним, что
R=
A%
B).
Потом, аналогично, свести эту чуть менее сложную задачу к ещё менее сложной, и так далее.
Практически это означает, что если начальник вас заставляет искать НОД(
A,
B),
нужно поделить с остатком, подозвать подчиненного и дать ему задание найти НОД(
B,
R).
Подчиненный сделает то же самое, т.е. даст аналогичное задание своему подчиненному.
Где-то там, на дне иерархии подчиненных, очередной подчиненный
получит задание с маленькими числами и сможет найти НОД перебором.
(В программировании это называется
рекурсивная функция).
Кстати, этот
подчиненный из глубин иерархии может и сам прибежать к вашему начальнику и принести
готовый ответ
6.
Пример 22
Найдем НОД(29,12). Находим остаток: 29%12=5.
Даем задание подчиненному: "А ну ка братец, найди мне НОД(12,5)".
Подчиненный находит остаток 12%5=2 и дает задание подподчиненному:
"А ну ка братец, найди мне НОД(5,2)".
Числа 5 и 2 достаточно маленькие, чтобы найти НОД. Он равен 1.
Итого: НОД(29,12)=1.
2.4 Алгоритм Евклида для нахождения равенства Безу
Основан на такой же рекурсии как и алгоритм нахождения наибольшего общего делителя
7.
Предположим, начальник дал нам
A,
B и велел найти
u,
v в равенстве
Вычисляем остаток
A=
B·
C +
R и даем задание своему подчинённому
пойти и найти числа в равенстве
|
B·(u1)+R·(v1)= |
НОД
| (B,R). |
|
Когда подчиненный принесет нам НОД и свои
u1,
v1, выражаем
подставляем в предыдущее равенство
|
B·(u1)+(A − B·C)·(v1)= |
НОД
| (B,R) |
|
и преобразуем в
|
A·( v1 ) + B·( u1−C·v1 ) = |
НОД
| . |
| (3) |
Таким образом, наше
u равно
v1 нашего подчиненного и наше
v=
u1−
C·
v1.
Как же подчиненный находит свои
u1 и
v1?
Да понятно как, он подзывает своего подчиненного и даёт ему аналогичное задание.
На дне иерархии подчиненных некий совсем уже низкопоставленный подчинённый получит
совсем маленькие
A,
B и найдет НОД,
u и
v просто перебором.
В программировании, эта цепочка подчиненных называется
стек вызова функции.
Вероятно, у вас на контрольной не будет под рукой подчинённого, и поэтому вам самому придется быть
своим подчинённым, давать задания самому себе, а стек вызова писать на бумажке в столбик.
Пример 23
Найдем числа в равенстве Безу для 29 и 12.
Производя деления с остатком (29=12·2 + 5, 12=5·2 + 2), построим стек:
Числа 5 и 2 достаточно маленькие, и понятно, что их НОД равен 1, и
соотношение Безу получится такое:
Начнем заполнять стек снизу вверх.
Первый шаг:
По формуле (3) найдем соотношение Безу для 12 и 5:
и заполним следующую строчку в стеке:
И, аналогично, еще одну строчку:
Итак, соотношение Безу найдено:
29·(−7 )+ 12·( 17 )=1.
(Читерская подсказка: заметили, как число из второй скобки переползает в первую строчкой выше?
Ну так это не случайность, а формула (
3). И число во второй скобке
можно находить, просто решая уравнение
с одной переменной).
Если мы собираемся производить вычисления со стозначными числами, то неплохо бы заранее
прикинуть размеры этого стека. Погуглив Википедию, можно узнать, что в алгоритме Евклида
за два шага числа уменьшаются примерно в два раза, т.е для стозначных чисел понадобится
примерно 800 подчиненных.
3 Всякая всячина
Тут будет то, что по какой-либо причине не поместилось в предыдущие главы.
3.1 Проблема плохого начальника
Предположим
,
начальник
задал вам математическую задачу. Вы её решали, решали и решили.
Принесли решение начальнику, а он и говорит:
"Чем докажешь, что решал? Может ты просто число какое-то наугад написал и теперь денег моих хочешь?"
И тогда вы медленно, по пунктам показываете этому нехорошему человеку, как именно вы решали.
А он медленно и занудно на калькуляторе проверяет все вычисления а потом и говорит:
"А за что деньги-то платить?
Все эти вычисления я сам только что проделал своими собственными руками, лучше я сам себе заплачу".
В некоторых случаях проблема разрешима. Например, если задали "решать квадратное уравнение через дискриминант",
вы можете торжественно сказать "
Чтобы проверить, надо подставить!".
Потом радостно, на глазах начальника подставить корни в уравнение и доказать, что ответ правильный.
Конечно, нехороший начальник вычтет из зарплаты стоимость трёх умножений и двух сложений, но
остальные деньги (после вычета налогов), наверное, отдаст.
Отсюда мораль: недостаточно уметь находить правильный ответ, нужно ещё уметь
находить легко проверяемое
доказательство правильности ответа.
3.2 Невозможное вычисление
Как
известно, компьютеры стали более лучше
одеваться вычислять
и почти достигли гиперзвука.
Олимпиард
операций в наносекунду скоро уже не предел.
Есть ли такие задачи, которые компьютеры никогда вычислять не смогут?
Предположим, наш супер процессор настолько быстр, что совершает
одну операцию за время прохождения
светом расстояния, равного радиусу атома (10
−19 секунд).
Предположим, мы никуда не торопимся, и 13.7 миллиардов (1.37·10
10) лет машинного
времени (это возраст Вселенной
) нас не пугают.
Один год это 60·60·24·365=31536000 ≈ 3·10
7 секунд.
Простые вычисления показывают, что даже в этом случае больше 4.3·10
36 операций не сделать.
И даже если сделать сверх многопроцессорный сверх компьютер с 1.3·10
50 процессорами
(столько атомов в земном шаре),
за гугол
(10
100) операций всё равно не вылезти.
Так что, если для решения задачи требуется гугол операций, можно расслабиться и ничего не делать.
Упражнение 8
Сколько тысяч миллиардов возрастов Вселенных понадобится этому
сверх многопроцессорному сверх компьютеру для подбора стозначного пароля
состоящего только из цифр?
Ответы на упражнения
Упр. 1.
Ответ:
x=4. Проверка: 4+3=7=5+2=2.
Упр. 2.
Ответ:
x=39. Проверка: 33·39 + 25 = 1312 = 32 ·41 + 0 = 0.
Упр. 4.
Ответ: Можно. Получится 4.
Упр. 8.
Ответ: Не меньше тысячи.
Предметный
указатель
- %, 1.1, 1.6,
2.1, 2.3
- RSA, 1.7
- Безу
- соотношение, 2.2
- Википедия, 1.4
- НОД, 2.2
- Эль-Гамаль, 1.7
- алгоритм извлечение корня,
1.5
- взаимно простые числа, 2.2
- возведение в степень, 1.4,
1.5
- быстрое, 1.4
- в кольце вычетов,
1.1
- в обычных числах,
1.0
- возраст Вселенной, 3.2
- вычитание, 1.2
|
- гугол, 3.2
- деление
- в кольце вычетов,
1.3,
1.3
- деление с остатком, 1.1,
2.1
- делимое
- деление с остатком,
1.1,
2.1
- делитель, 2.2
- деление с остатком,
1.1,
2.1
- делится, 2.2
- доказательство правильности ответа,
2.2,
3.1
- извлечение корня, 1.5,
1.6
- как найти:
- корень в кольце вычетов,
1.5,
1.5,
1.6
- обратное в кольце вычетов,
1.3,
1.3
- произведение в кольце вычетов,
1.1
- разность в кольце вычетов,
1.2,
1.2
- степень в кольце вычетов,
1.4,
1.4
- сумму в кольце вычетов,
1.1
- частное в кольце вычетов,
1.3,
1.3
- кольцо вычетов, 1.0
|
- наибольший общий делитель,
2.2
- обратное число, 1.3
- в кольце вычетов,
1.3
- олимпиард, 3.2
- остаток
- деление с остатком,
1.1,
1.6,
2.1
- плохой начальник, 2.2,
3.1
- противоположное число, 1.2
- прямое произведение, 1.6
- рекурсивная функция, 2.3
- рекурсия, 2.3
- сложение
- в кольце вычетов,
1.1
- в обычных числах,
1.0
- соотношение Безу, 1.6,
2.2
- стек
- вызова функции, 2.4
|
- умножение
- в кольце вычетов,
1.1
- в обычных числах,
1.0
- частное
- деление с остатком,
1.1,
2.1
- числа
- в виде велосипедика,
1.6
- взаимно простые, 1.6,
1.6
- кольцо вычетов, 1.0
- ненормальные, 1.0
- обратные, 1.3
- обычные, 1.0
- отрицательные, 1.2
- простые, 1.5
- противоположные, 1.2,
1.2
- прямое произведение колец вычетов,
1.6
- целые, 2.0
|
1Алгоритмы быстрого возведения в степень.
http://goo.gl/yae8h9
2Погуглите, чтоб узнать.
http://goo.gl/Iut1et
3Не пугайтесь, по-научному это
называется
прямое произведение колец вычетов
4По научному это называется "
изоморфизм".
5"Socialist millionaires", на русский
язык эту статью в Википеди пока никто не соизволил перевести.
http://goo.gl/laIOhg
6В программировании это
называется
хвостовая рекурсия
7Если вы еще не
читали раздел
2.3, то сейчас самое время это сделать.
File translated from
TEX
by
TTH,
version 4.14.
On 11 Oct 2023, 12:40.